
One of the most stubborn questions in computer science and mathematics is whether these “NP” problems, including the knapsack problem, are truly different from “P” problems, those that can be solved in what is called polynomial time. This property is known as “NP completeness.” Therefore, if one could be solved and verified efficiently with an algorithm, they all could. Some NP problems like the knapsack example have a special property: In the early 1970s, Stephen Cook and Richard Karp showed that a variety of NP problems could be converted into a single problem of formal logic. “We think you could cover the entire Earth with processors and run them until the heat death of the universe and still fail to solve relatively small instances of appropriate versions of these problems,” says Noah Stephens-Davidowitz, a Microsoft Research Fellow at the Simons Institute in Berkeley, California. Given an indefinite amount of time, a computer could use brute force to optimize large cases like this, but not on timescales that would be practical. For example: Given a list of 1 million museum artifacts with their weights and monetary values, and a backpack limited to 25 pounds, a computer would have to run through every possible combination to generate the single one with the most lucrative haul. “The problem the theoreticians started to look at was how efficiently a particular task can be carried out on a computer,” writes Keith Devlin in the book The Millennium Problems. By definition, NP problems also have solutions that are easy to verify (it would be trivial to check that a particular list of items does, in fact, fit in a backpack). The knapsack problem belongs to a class of “NP” problems, which stands for “nondeterministic polynomial time.” The name references how these problems force a computer to go through many steps to arrive at a solution, and the number increases dramatically based on the size of the inputs-for example, the inventory of items to choose from when stuffing a particular knapsack. Today, as technology capable of shattering the locks on our digital communications loom on the horizon, the knapsack problem may inspire new ways to prepare for that revolution.
Knapsack problem cracked#
Researchers once took advantage of the problem’s complexity to create computer security systems, but these can now be cracked since the problem has been so well studied. “From a practical perspective, the knapsack problem is ubiquitous in everyday life.”

“A lot of problems we face in life, be it business, finance, including logistics, container ship loading, aircraft loading - these are all knapsack problems,” says Carsten Murawski, professor at the University of Melbourne in Australia. And the knapsack problem is more than a thought experiment.

This fictional dilemma, the “knapsack problem,” belongs to a class of mathematical problems famous for pushing the limits of computing. But the more objects there are, the more taxing this calculation becomes for a person-or a computer. How do you choose among the objects to maximize your loot? You could list all the artifacts and their weights to work out the answer by hand.
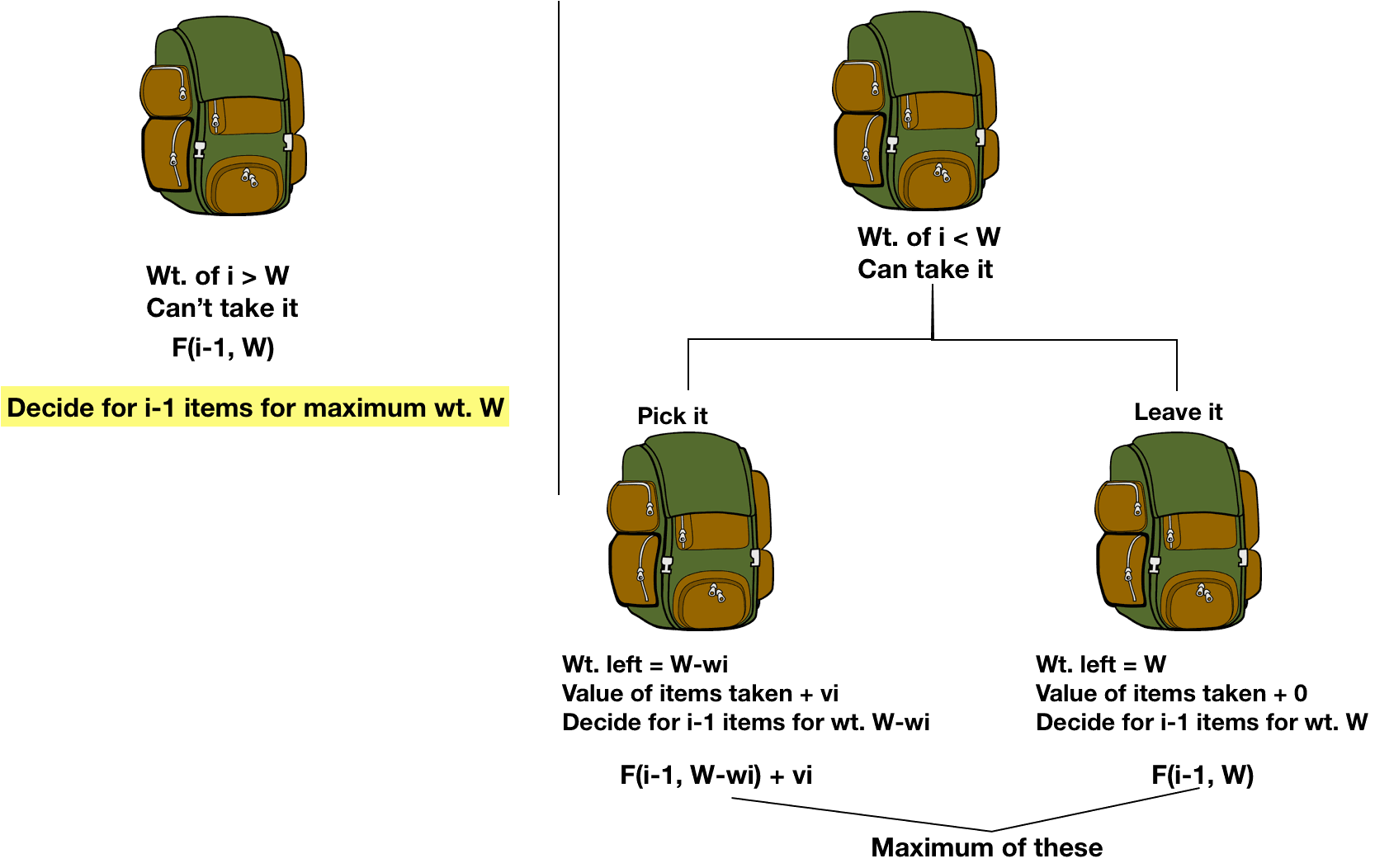
Your goal should be to get away with the most valuable objects without overloading your bag until it breaks or becomes too heavy to carry. You're new at this, so you only brought a single backpack. Imagine you’re a thief robbing a museum exhibit of tantalizing jewelry, geodes and rare gems.


 0 kommentar(er)
0 kommentar(er)
